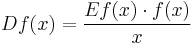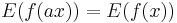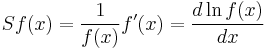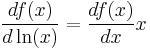Elasticity of a function
In mathematics, elasticity of a positive differentiable function f of a positive variable (positive input, positive output) at point x is defined as[1]
or, in terms of percentage change
Intuitively, it is the percentage change in output for a percentage change in input – percentages only making sense if the quantities are all positive.[2] Formally, it is the ratio of the incremental change of the logarithm of a function with respect to an incremental change of the logarithm of the argument. This definition of elasticity is also called point elasticity, and is the limit of arc elasticity between two points.
Elasticity is widely used in economics; see elasticity (economics) for details.
Contents |
Rules
Rules for finding the elasticity of products and quotients are simpler than those for derivatives. Let f, g be differentiable. Then[1]
The chain rule is similar to the derivative
The derivative can be expressed in terms of elasticity as
Let a and b be constants. Then
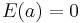
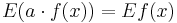 ,
,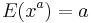 , and also
, and also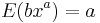 .
.
Estimating Point Elasticities[3]
PED can also be expressed as (dQ/dP)/Q/P or the ratio of the marginal function to the average function for a demand curve Q = f( P). This relationship provides an easy way of determining whether a point on a demand curve is elastic or inelastic. The slope of a line tangent to the curve at the point is the marginal function. The slope of a secant drawn from the origin through the point is the average function. If the slope of the tangent is greater than the slope of the secant (M > A) then the function is elastic at the point. [4]]If the slope of the secant is greater than the slope of the tangent then the curve is inelastic at the point.[5] If the tangent line is extended to the horizontal axis the problem is simply a matter of comparing angles formed by the lines and the horizontal axis. If the marginal angle is numerically greater than the average angle then the function is elastic at the point. If the marginal angle is less than the average angle then the function is inelastic at that point. If you follow the convention adopted by economist and plot the independent variable on the vertical axis and the dependent variable on the horizontal axis then the marginal function will be dP/dQ and the average function will be P/Q meaning that you are deriving the reciprocal of elasticity. Therefore opposite rules would apply. The tangency line slope would be dP/dQ and the slope of the secant would be the numerical value P/Q. This method is not limited to demand functions it can be used with any functions. For example a linear supply curve drawn through the origin has unitary elasticity (if you use the method the marginal function is identical to the slope). If a linear supply function intersects the y axis then the marginal function will be less than the average and the function is inelastic at any point and becomes increasingly inelastic as one moves up the curve.[6] With a supply curve that intersects the x axis then the slope of the curve will exceed the slope of the secant at all point meaning that the M > A the slope is elastic and will become increasingly elastic as one moves up the slope. Again this assumes that the dependent variable is drawn on the Y axis.
Semi-elasticity
A semi-elasticity (or semielasticity) gives the percentage change in f(x) in terms of a change (not percentage-wise) of x. Algebraically, the semi-elasticity S of a function f at point x is [7][8]
An example of semi-elasticity is modified duration in bond trading.
The terms Semi-elasticity is also sometimes used for the change if f(x) in terms of a percentage change in x[9] which would be
See also
References
- ^ a b Sydsaeter, Knut and Hammond, Peter, Mathematics for Economic Analysis, Prentice Hall, 1995, pages 173-175.
- ^ More generally, the elasticity can be defined if the input or output is consistently negative, or simply away from any points where the input or output is zero, but in practice the elasticity is used for positive quanitities.
- ^ Chiang & Wainwright, Fundamental Methods of Mathematical Economics 4th ed. Page 192-93. McGraw-Hill 2005
- ^ Chiang & Wainwright, Fundamental Methods of Mathematical Economics 4th ed. Page 192-93. McGraw-Hill 2005
- ^ Chiang & Wainwright, Fundamental Methods of Mathematical Economics 4th ed. Page 192-93. McGraw-Hill 2005
- ^ Chiang & Wainwright, Fundamental Methods of Mathematical Economics 4th ed. Page 192-93. McGraw-Hill 2005
- ^ Jeffrey Wooldridge. Introductory Econometrics: A Modern Approach, 2nd Edition. ISBN 0324113641.
- ^ Lawrence Henry White. The theory of monetary institutions. ISBN 0631212140.
- ^ http://www.stata.com/help.cgi?margins
- Yves Nievergelt, The Concept of Elasticity in Economics, SIAM Review, Vol. 25, No. 2 (Apr., 1983), pp. 261–265
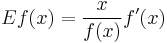
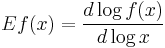
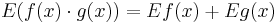
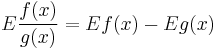
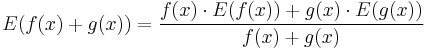
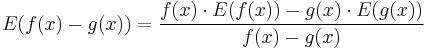
![E (f \circ g)(x) = [ E(f(x)) \circ g(x) ] \cdot E(g(x))](/2012-wikipedia_en_all_nopic_01_2012/I/e64f4910dd8dbf5dca2637771f0c1f67.png)